Sine and Cosine

Before going on to the next post about acceleration, I need to explain sine (sin) and cosine (cos). First, let’s take a triangle. This one will do nicely.



You need to have a standard set of directions, though, so let’s put the triangle on a set of horizontal and vertical axes.



On the first triangle, you can measure sine and cosine from either point A or point C. The little letters a, b and c stand for the lengths of the sides. A and C also get numbers, the size of the angles in degrees. Now how do they all relate to each other?

sinA=a/b
cosA=c/b
sinC=c/b
cosC=a/b

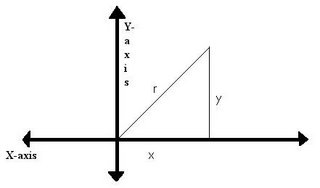
Back in trigonometry (or was it algebra?) the teacher taught us an acronym: SohCahToa. That says three things. Number one, sine equals opposite over hypotenuse. Second, cosine equals adjacent over hypotenuse. Lastly, there’s tangent, but I’ll write about that later. Now, about the triangle I drew on the axes, that’s what I wanted to get to because that is the best one for what I’m going to put in the next post. On that triangle, you always measure from the origin, the place where the two axes cross, and you use the Greek letter θ (theta) to stand for the size of the angle. You only need two things for that triangle.

sinθ=y/r
cosθ=x/r

They’re the same as on the first triangle, just with different names for the variables.